Faire de l’art avec des mathématiques – L’Art Fractal
L’art Fractal représente l’alliance de l’art et des mathématiques. Cette forme d’art récent utilise des ordinateurs pour fabriquer des images à partir de formules mathématiques. Les oeuvres d’art fractal présentent un aspect souvent géométrique, des motifs compliqués et une grande richesse de détails. Mais comment fait-on pour créer des images à partir de formules mathématiques ?
Tout d’abord que veut-dire « Fractal » ?
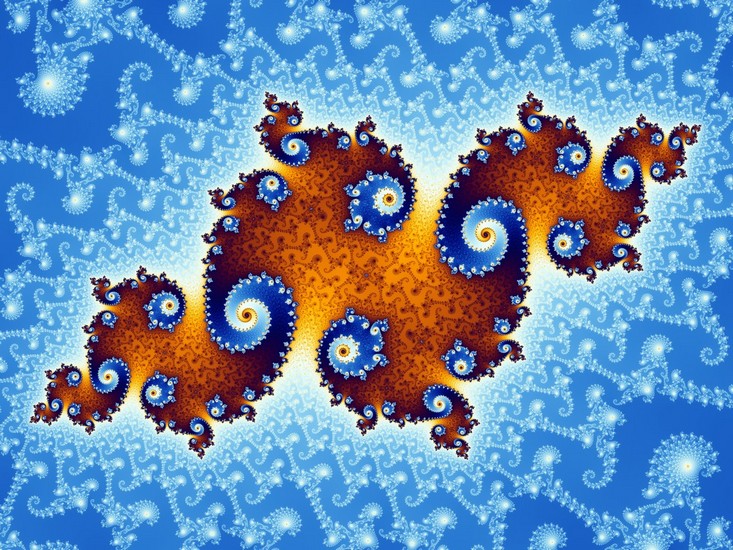
Dans les années 1970, l’informaticien Benoit Mandelbrot découvre l’une des images fractales les plus célèbres : l’ensemble de Mandelbrot.

Cette découverte est permise par le développement de l’informatique, notamment grâce à la puissance de calcul des ordinateurs. Elle a également lieu dans le contexte scientifique de l’élaboration de la théorie du Chaos qui étudie les phénomènes dynamiques (turbulences, tourbillons dans un fluide, oscillation, forme des nuages…).
De même, la géométrie fractale se retrouve dans les formes de la nature aux contours complexes (flocon de neige, feuille d’un arbre, forme des nuages, tourbillons, arborescence du réseau sanguin, forme des côtes maritimes…) qu’il était difficile de modéliser avec les outils mathématiques précédents.

Caractéristiques des images fractales
La dimension fractale
L’appellation « fractal » renvoie à l’idée d’une dimension non entière, fractionnée. Jusque dans les années 1960, les mathématiques étudiaient des objets décomposables à l’aide de dimension entière :
un point : dimension 0
une ligne : dimension 1
un plan : dimension 2
un volume : dimension 3
Mais imaginons une feuille de papier. Elle représente un plan, donc possède une dimension égale à 2. Si nous froissons cette feuille, elle occupe maintenant un volume (dimension 3), mais n’est pas un volume car nous ne pouvons pas « remplir » la feuille froissée avec une matière comme on remplirait un récipient. La dimension de la feuille froissée est donc comprise entre 2 et 3 : 2,568 par exemple. Une dimension fractale !
Les objets fractals possèdent ainsi des formes complexes, irrégulières, avec des contours pliés et repliés sur eux-mêmes.
L’auto-similarité
Malgré sa complexité, un objet fractal présente des détails similaires. En zoomant à l’intérieur d’une fractale, on retrouve le même motif d’ensemble répété à différentes échelles, et à l’infini. Une partie est donc semblable au tout. Cette propriété s’appelle l’invariance d’échelle.

Typologie
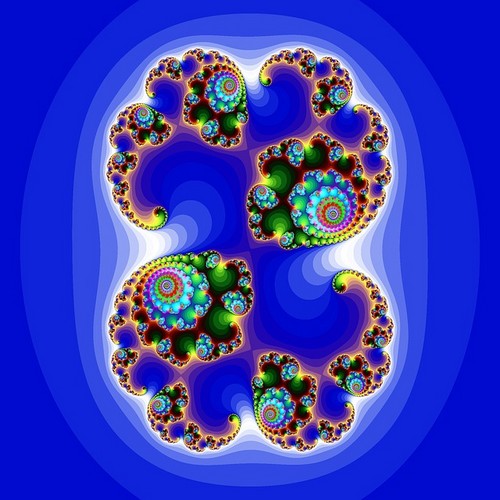
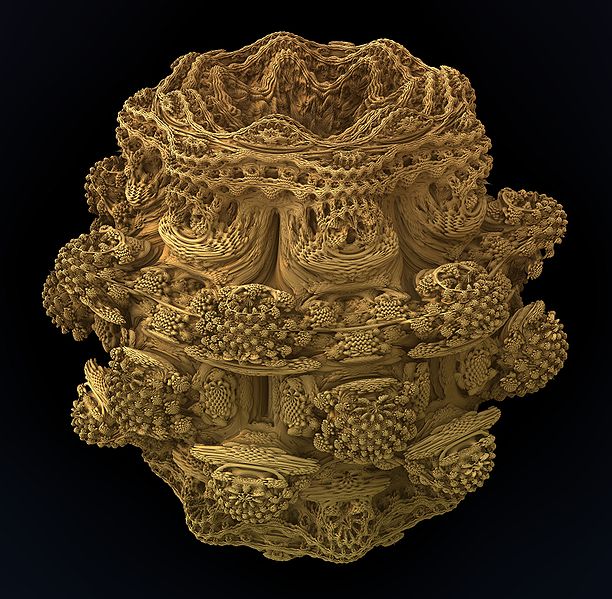
Fractales par récurrence

Les IFS, systèmes de fonctions itérées



Génération des images fractales, « La simplicité engendre la complexité »
La construction des images fractales repose sur l’utilisation d’Algorithme exécuté en boucle. Il s’agit d’un processus itératif répétant une série d’opérations simples.
Fractales par récurrence
Pour chaque point de l’espace, les coordonnées du point sont passées dans une équation. Le résultat est ensuite réinjecté dans la même équation. L’opération est réalisée plusieurs fois de suite (itérations). Puis on teste le résultat:
Si le résultat tend vers l’infini, alors le point de départ n’est pas dans l’ensemble : il est colorié en blanc.
Si le résultat reste stable, ou périodique, alors le point de départ est dans l’ensemble : il est colorié en noir.
Pour les points situés sur la frontière, il est plus difficile de déterminer si ils sont dans l’ensemble ou en dehors. Il faut alors réaliser davantage d’itérations. En fonction du nombre d’itérations nécessaires pour déterminer le point, celui-ci est colorié en différentes nuances. Ce sont les points de cette frontière qui donnent à la fractale sont aspect compliqué et enchevêtré.
Pour dessiner l’ensemble de Mandelbrot, on utilise des nombres complexes qui représentent chacun un pixel du plan. On exécute l’équation suivante pour chaque point : Zn+1 = Zn2 + C , avec Z0 = 0.
Les IFS, systèmes de fonctions itérées
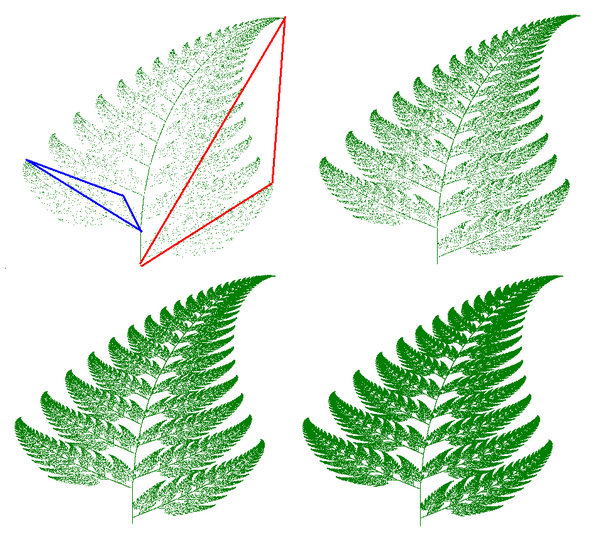
La construction d’image s’effectue ici par copie d’elle-même. Mais à chaque copie, l’image copiée subit une transformation géométrique (une transformation linéaire représentée en mathématique par une fonction linéaire). Ces transformations peuvent être des rotations, des aplatissement, des cisaillements… Les copies sont également contractées avant d’être replacées sur l’image d’origine. Le processus est répété jusqu’à former une image.
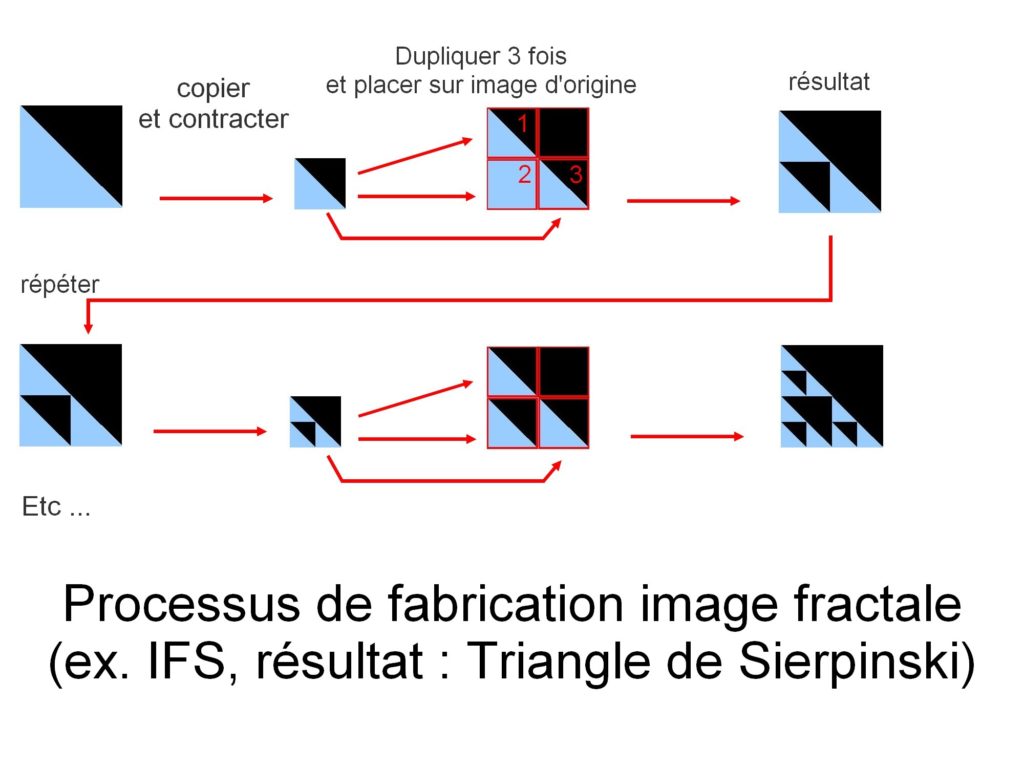
Cet exemple aboutit à l’image du triangle de Sierpinski.
Autre exemple, la génération du flocon de Koch.

Les IFS permettent de produire facilement des images rappelant des objets naturels, comme des arbres, fougères…